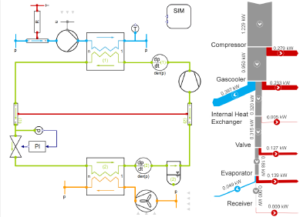
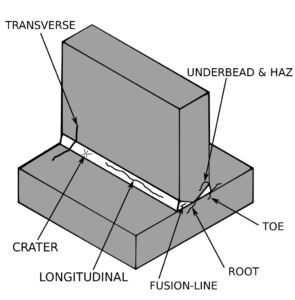
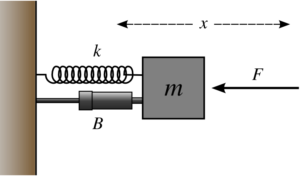
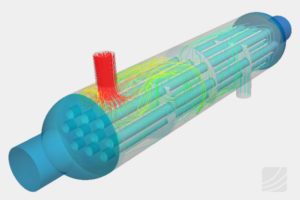
Significance of Courant number for stability and convergence of CFD simulations
Significance of Courant Number for Stability and Convergence of CFD Simulations
What is Courant number ?
Courant-Friedrichs-Lewy (CFL) condition is absolutely essential in solving the partial differential equations. This non dimensionless number arises while solving the time marching problems. This condition is named after the respective scientists Richard Courant, Kurt Friedrichs, and Hans Lewy who introduced it in 1928. It is given by:
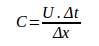
Where C is the courant number, U is the dependent variable, Δt is the time interval and Δx is the distance between any two consecutive nodes.
Courant number can be controlled by altering the time or space interval. When the space interval is reduced or time interval is increased the courant number increases. Since courant number governs the stability of a problem in an explicit method it is very important to choose the intervals precisely.
What does Courant number do ?
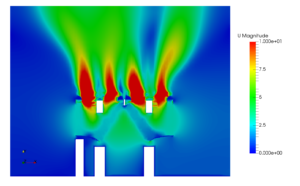
The CFL condition presents itself in those equations of the finite-difference approximation of general partial differential equations which govern the advection phenomenon. In an explicit time marching problem such as an one dimensional wave motion it depends upon the velocity, time step and the length of the interval between two nodes. Courant number does not present itself in steady state problems and it governs the stability of a numerical method only in transient equations. Its accumulation is not restricted to one dimensional problems alone. It also occurs in two dimensional problems. There can be finite number of courant numbers for finite number of dimensions respectively. Since problems in reality are limited to three dimensions, there can be a maximum of three courant numbers respectively.
Courant Number and Stability:
In explicit methods that are conditionally stable, CFL criteria might be necessary but not necessarily be sufficient for convergence. The values of courant numbers might vary in accordance to the method that is used to solve the discretized equations. In general the explicit methods depend greatly on courant number for their stability. Whereas, the implicit methods are insensitive with changes in courant number. When an explicit method is used, larger values of courant number are not tolerated by the numerical domain. The stability criteria for a typical time marching problem such as a one dimensional wave equation is that courant number must not be greater than one. For conditionally stable methods depending on the intensity of the initial conditions, an user has to decrease the CFL to a value as low as 0.1 to 0.5 to get started. Once the startup transients are reduced you can start increasing the Courant number again.You may find that a lower CFL is required during startup (when changes in the solution are oscillating), but it can be increased as the solution progresses. This is why these methods are called unconditionally stable. In robust CFD solvers the facility to introduce courant number will be available in the solutions control option. So, CFL criteria plays a vital role in determining the stability of the solution depending on the method used to solve the equations.
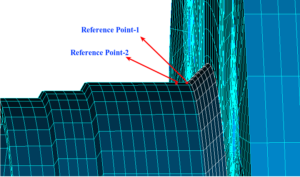
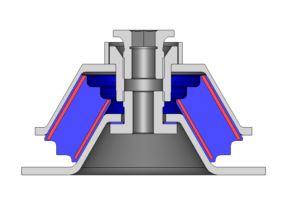
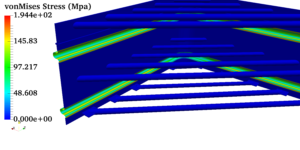
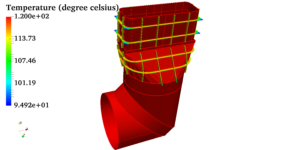
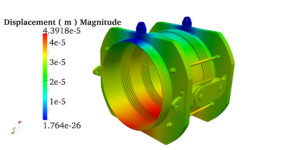
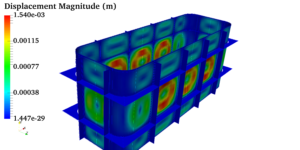Pressure vessels, pipes, expansion joints etc. are basic equipments for process industries. Pressure vessels are vessels working under internal, external or vacuum pressure, and possibly subjected to high temperature. Proper design and analysis is very important for the pressure vessels, as their failure can cause lot of hazards. Codes/ standards are used in the design phase, followed by analysis to ascertain stresses are within the allowable range. ASME provides wide range of guidelines for the proper design of such vessels.
